Сортування

При розв’язуванні задач, пов’язаних з обробкою масивів, виникає необхідність виконувати сортування його елементів. Наприклад, у 2012-2013 навчальному році на обласній олімпіаді друга задача “День святого Валентина” розв’язувалась з використанням сортування. Над методами сортування працювало багато вчених не один рік, і придумали їх багато.
Розглянемо деякі з методів, що дають змогу впорядкувати елементи таблиць.
Всі існуючі методи сортування можна поділити на три групи:
• обмінні сортування — виконується обмін між двома елементами масивів, якщо відповідні елементи розташовані у вихідному масиві невпорядковано; процес повторюється або певну кількість разів, або доки елементи в масиві не стануть впорядкованими;
• сортування вибором — в масиві обирається елемент з певними властивостями а потім вибраний елемент ставиться на своє місце;
• сортування вставками— послідовно вибираються елементи з масиву і після визначення їх місця у впорядкованому наборі даних вставляються безпосередньо на своє місце.
Обмінне сортування. Метод "бульбашки"
Розглянемо обмінне сортування методом «бульбашки». Цей метод вважається найпростішим і в ньому бажано розібратися.
Потрібно пробігтись по масиву чисел і порівняти два елементи. Нехай впорядкування здійснюється за зростанням. При порівнянні, якщо більший елемент лівіше, то він міняється місцем з іншим елементом. Програма має вигляд:
for i:=1 to n-1 do
for j:=1 to n-1 do
if a[j]>a[j+1] then begin
r:=a[j];
a[j]:=a[j+1];
a[j+1]:=r;
end;
Приклад:
5 7 4 1
Перший раз, коли виконається внутрішній цикл, буде:
5 4 1 7
Найбільший елемент переміститься в кінець (сплив, наче мильна бульбашка), але масив іще не впорядкувався, тому у нас в програмі потрібно два цикли. Оскільки нам ті елементи в кінці, що впорядкувались, можна не трогать, тому внутрішній цикл можна зробити до n-i
for i:=1 to n-1 do
for j:=1 to n-i do
if a[j]>a[j+1] then begin
r:=a[j];
a[j]:=a[j+1];
a[j+1]:=r;
end;
Другий раз, коли виконається внутрішній цикл, буде:
4 1 5 7
За третім разом:
1 4 5 7
Бульбашкове сортування зберігає взаємний порядок однакових значень (тобто є стійким).
Метод швидкого сортування
Можна досить успішно користуватись даним алгоритмом, але дуже часто іде перевищення часу, тому розглянемо метод швидкого сортування.
Перший алгоритм швидкого сортування був розроблений у 1960 році Хоартом.
Якийсь елемент береться за зразок (еталон), нехай позначимо z. Масив розбивається на дві ділянки: ліву і праву. Елементи в лівій ділянці мають значення не більше зразка, а у правій – не менше зразка. Після цього окремо відсортовується кожна ділянка. Позначимо L – лівий кінець масиву, а R – правий кінець масиву. z беремо, як середній елемет z:=a[(L+R) div 2];
Беремо два індекси: i, j. Спочатку i:=L; j:=R; Далі вони рухаються назустріч один одному. Значення менші z (хороші) в лівій частині пропускаються, а на інших значеннях (поганих) зупиняється. Якщо і<=j, то обидва індекси стоять на поганих значеннях. Значення з цими індексами міняються місцями, а індекси зсуваються назустріч один одному. Так буде до тих пір, поки i не стане більше j. Далі обидві ділянки сортуємо рекурсивно, поки вони більші одиниці. Якщо довжина 1, то цю ділянку уже відсортовано.
procedure as ( L,R:longint) ;
var i,j,z,r1:longint;
begin
z:=a[(L+R) div 2];
i:=L;
j:=R;
repeat
while a[i]<z do i:=i+1;
while a[j]>z do j:=j-1;
if i<=j then begin
r1:=a[i];
a[i]:=a[j];
a[j]:=r1;
i:=i+1;
j:=j-1;end
until i>j;
if j>L then as (L,j);
if i<R then as (i,R);
end;
Швидке сортування не зберігає взаємного порядку однакових значень.
Вдосконалити даний алгоритм можна розумним вибором зразка. Один із способів: знайти середнє із значень лівого, правого і серединного.
if a[L]>a[(L+R) div 2] then begin
r1:=a[L]; a[L]:=a[(L+R) div 2]; a[(L+R) div 2]:=r1;
end;
if a[(L+R) div 2 ]>a[R] then begin
r1:=a[(L+R) div 2]; a[(L+R) div 2]:=a[R]; a[R]:=r1;
end;
if a[L]>a[(L+R) div 2] then begin
r1:=a[L]; a[L]:=a[(L+R) div 2]; a[(L+R) div 2]:=r1;
end;
Кого зацікавила дана тема, розгляньте сортування “злиттям” і пірамідальне сортування. Дані методи чудово описані в статті І. Скляр, А. Скляр. “І знову сортування”.
Пірамідальне сортування
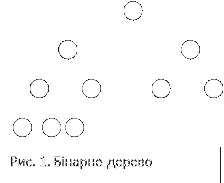
Пірамідальне сортуваня (або сортування за допомогою купи) використовує таку структуру даних, як врівноважене бінарне дерево або, як його ще називають, купа.
Купою називають масив, що має деякі властивості. Щоб легше було їх уявити, представимо масив, як бінарне дерево (дивись рис. 1). Кожна його вершина відповідає елементу масиву. У вершини з номером i дітьми, якщо вони існують, будуть елементи 2i та 2i+1, а батьком – i div 2. Перший елемент масиву буде коренем дерева.
Головною властивістю купи, яка має обов’язково виконуватись, є правило: A[i div 2]³A[i] (окрім кореня). Звідси випливає, що найбільший елемент дерева знаходиться у корені дерева.
Висотою вершини дерева називається кількість ребер у найдовшому шляху з цієї вершини вниз до листа (вершини, у якої немає синів). Висота дерева, що складає купу з N елементів, дорівнює приблизно log2 N.
Суть методу впорядкування за допомогою купи базується на тому факті, що корінь правильно побудованої купи буде максимальним її елементом. Тому перед впорядкуванням ми робимо з масиву правильну купу, а далі, у процесі сортування, помістивши кореневий (перший) елемент на своє місце, відновлюємо серед решти елементів масиву основну властивість купи.
Алгоритм здається зовсім простим:
Procedure HeapSort (var A:IntArray;N:integer);
Begin
BuildHeap (A,N);
For i:=N downto 2 do
Begin
Swap (A[1],A[i]);
RestoreHeap (A,i-1,N);
End;
End;
При первинному створенні купи з масиву даних (процедура BuildHeap) ми проходимо по всім елементам-батькам масиву і відновлюємо у їхніх гілках основну властивість купи:
Procedure BuildHeap (var A:IntArray;N:integer);
Var i:integer;
Begin
for i:=N div 2 downto 1 do
RestoreHeap (i,N);
End;
Коли ж ми прибрали кореневий елемент, виникає необхідність відновити правильну купу (підпрограма RestoreHeap). Ідея цього відновлення проста: якщо основна властивість у новому кореневому елементі не виконується, то більший з синів обмінюється з батьком, після чого основна властивість перевіряється і у сина.
Procedure RestoreHeap (var A:IntArray;C,N:integer);
Var MaxSon:integer;
Begin
MaxSon:=C;
If (C*2<=N)and(A[C]<A[C*2])
then MaxSon:=C*2;
If (C*2+1<=N)and(A[MaxSon]<A[C*2+1])
then MaxSon:=C*2+1;
If MaxSon<>C
then Begin
Swap (A[C],A[MaxSon]);
RestoreHeap (A,MaxSon,N);
End;
End;
Сортування “злиттям”
Одною з найпривабливіших властивостей цього методу сортування є те, що він впорядковує N елементів за час, пропорційний Θ(N log N), незалежно від характеру вхідних даних. Метод є стійким і це схиляє чашку терезів у його сторону в тих випадках, коли дана обставина є дуже важливою. Але одним із найголовніших недоліків його є той факт, що в простій реалізації необхідний додатковий масив для злиття. Цю перешкоду можна і обійти, але зробити це досить важко, причому знадобляться додаткові витрати часу, які в загальному випадку себе не виправдовують. Один з варіантів обходу додаткових витрат був запропонований Бетчером, але його ми розглянемо пізніше.
В основі базового алгоритму сортування лежить така корисна і необхідна у деяких задачах операція, як злиття двох впорядкованих підмасивів у один (теж впорядкований). Це обернена до використаної у швидкому сортуванні (коли ми розбивали один масив на дві частини) операція.
Ця операція реалізується досить легко і зрозуміло. Можна уявити два підмасиви у вигляді стеків (створити курсори, що вказуватимуть номери “голів” і збільшувати їх, коли з стека “забирають” елемент). Тоді достатньо у черговий елемент нового масиву заносити менше значення з двох “голів” (або, якщо один зі стеків став порожнім, значення “голови” іншого стека).
Під час сортування ми “зливатимемо” дві сусідні частини одного масиву вхідних даних, тому в підпрограму Merge передаємо лише границі підмасивів (L – початок першої частини; M – початок другої частини; R – кінець другої частини):
Procedure Merge (var A:IntArray;L,M,R:integer);
Var i,Cur1,Cur2:integer;
aux:array [1..MaxN] of integer;
Begin
Cur1:=L; Cur2:=M+1;
For i:=L to R do
Begin
If Cur1>M-1 then
Begin
aux[i]:=A[Cur2];
Inc (Cur2);
End else
If Cur2>R then
Begin
aux[i]:=A[Cur1];
Inc (Cur1);
End else
If A[Cur1]>A[Cur2] Then
Begin
aux[i]:=A[Cur1];
Inc (Cur1);
End else
Begin
aux[i]:=A[Cur2];
Inc (Cur2);
End;
End;
For i:=L to R do A[i]:=aux[i];
End;
Самого ж сортування “злиттям” розрізняють декілька методів.
Злиття зверху донизу. Реалізація методу, як і попередні швидкі сортування, містить рекурсію. Вона полягає у тому, що спочатку впорядковуються дві частини масиву (L..(L+R)/2 та (L+R)/2+1..R), а потім ці частини зливаються за допомогою описаного вище алгоритму.
Програма прозора:
Procedure MergeSort (var A:IntArray;L,R:integer);
Begin
If L>=R then Exit;
MergeSort (A,L,(L+R) div 2);
MergeSort (A,(L+R) div 2+1,R);
Merge (A,L,(L+R) div 2+1,R);
End;
Злиття знизу догори. Цей метод не використовує рекурсію. Спочатку весь масив розбивається (умовно) на частини довжиною в один елемент, які після цього попарно зливаються. Коли маленькі частинки злито, процес повторюється для отриманих вдвічі більших частин.
Procedure MergeSort (var A:IntArray;N:integer);
Var m,i:integer;
Begin
m:=1;
While m<N do
Begin
i:=0;
While i+m<=N do
Begin
Merge (A,i+1,i+m,Min (i+2*m,N));
i:=i+2*m;
End;
m:=2*m;
End;
Merge (A,1,N div 2,N);
End;
Парно-непарне злиття. Алгоримт був розроблений Бетчером у 1986 році під назвою Batcher’s odd-even sort.
Цей метод є неадаптивним (послідовність виконуваних дій залежить тільки від кількості вхідних даних, а не від значень ключів), тобто він може бути записаний у вигляді простого переліку операцій порівняння-обміну (як, наприклад, сортування “бульбашки” чи Праттова версія сортування методом Шелла).
В основі його лежать дві обернені операції: ідеальне тасування та зворотнє ідеальне тасування. Це метод спеціального призначення і його рідко використовують, перш за все тому, що зрозуміти, чому він працює правильно, досить важко.
Операція ідеального тасування переупорядковує масив так, як може перетасувати колоду карт тільки великий спеціаліст цієї справи: колода ділиться точно пополам, після чого карти по одній (починаючи з верхньої половини колоди) беруться з кожної частини і складаються в одну стопку.
Procedure Shuffle (var A:IntArray;L,R:integer);
Var i:integer;
aux:array [1..MaxN] of integer;
Begin
for i:=0 to R-L do
if i mod 2 = 0
then aux[l+i]:=A[l+i div 2]
else aux[l+i]:=A[(l+r) div 2+1+i div 2];
for i:=L to R do A[i]:=aux[i];
End;
Зворотнє ідеальне тасування виконує обернену операцію: з колоди карти беруться по порядку по одній і по черзі кладуться то поверх нової стопки, то під низ її.
Procedure Unshuffle (var A:IntArray;L,R:integer);
Var i:integer;
aux:array [1..MaxN] of integer;
Begin
For i:=0 to (L+R) div 2-L do
Begin
aux[L+i]:=A[L+i*2];
aux[(L+R) div 2+1+i]:=A[L+1+i*2];
End;
For i:=L to R do A[i]:=aux[i];
End;
Саме ж злиття Бетчера виконується за такою схемою:
1) зворотне ідеальне тасування (розбиття групи L..R на незалежні підгрупи вдвічі меншого розміру);
2) виконання того ж злиття Бетчера, але для кожної підгрупи елементів L..(L+R)/2 та (L+R)/2+1..R окремо;
3) ідеальне тасування (повернення елементів підгруп на початкове місце);
4) перевірка правильності розташування елементів у отриманому масиві та виправлення "помилок" сортування.
Procedure Merge (var A:IntArray;L,R:integer);
Var i:integer;
Begin
if (R=L+1)and(A[L]>A[R]) then
Swap (A[L],A[R]);
if R<=L+1 then Exit;
Unshuffle (A,L,R);
Merge (A,L,(L+R) div 2);
Merge (A,(L+R) div 2+1,R);
Shuffle (A,L,R);
i:=L+1;
while i<R do
Begin
If A[i]>A[i+1] then
Swap (A[i],A[i+1]);
Inc (i,2);
End;
End;
А алгоритм сортування Бетчера відрізняється від сортування злиттям тільки заміною звичайної процедури злиття запропонованою вище.
Іноді виникає ситуація, коли елементи масиву даних мають дещо незвичайні властивості, які можна використати для одержання надшвидких методів сортування аж до лінійної складності (Θ(N)).
Література: А. Ставинський, І. Скляр “Програмуємо правильно” частина 2.
Завантажити у форматі doc:

 Сортування теорія.doc
Сортування теорія.doc



